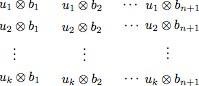Tag Archive | Truco
marzo 3, 2014  

Profundidad simplicial coloreada (¡finalmente resuelto!)


Un resultado clásico de Bárány en geometría discreta dice lo siguiente (donde \langle S \rangle se refiere a la envolvente convex de S)

Teorema (Carathéodory coloreado, Bárány 1982).

Dados d+1 conjuntos A_1, A_2, \ldots, A_{d+1} en \mathbb{R}^d y un punto y tal que y \in \langle A_i \rangle para cada i, existen puntos x_1 \in A_1, x_2 \in A_2, \ldots, x_{d+1} \in A_{d+1} de tal forma que y \in \langle x_1, x_2, \ldots, x_{d+1}\rangle.

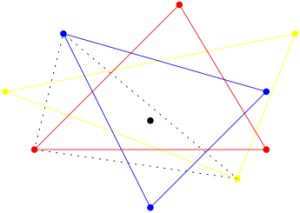
Por ejemplo, en el plano, si hay 3 triángulos monocromáticos que contienen un punto, hay un triángulo heterocromático que también lo atrapa.

Por ejemplo, en el plano, si hay 3 triángulos monocromáticos que contienen un punto, hay un triángulo heterocromático que también lo atrapa.

Una pregunta natural es: si se puede garantizar que hay un simplejo heterocromático que atrapa al punto, ¿cuál es la mínima cantidad \mu (d) de simplejos con esa propiedad que puedo garantizar?  Para esto vamos a suponer que cada conjunto contiene d+1 puntos y y está en el interior de las envolventes convexas (si no, considerando d+1 copias de y, solo obtenemos un simplejo atrapando al punto, por lo que sin suponer algún tipo de posición general el problema no es interesante).

El teorema que mencioné muestra que \mu (d) \ge 1, y la mejor cota superior que se conocía es \mu (d) \le d^2+1, por una construcción de Deza et al. [1], quienes conjeturaban que esta cota era óptima.  Hace poco acaba de salir un manuscrito de Pauline Sarrabezolles, dando una respuesta afirmativa a la conjetura.  Es decir, \mu (d) = d^2+1.

La idea de la demostración se basa en una reducción del problema geométrico a uno combinatorio, estudiando lo que se llaman «configuraciones octaedrales».  La idea de la reducción nace a partir de las siguientes dos observaciones

  • Una versión fuerte del teorema de Carathéodory coloreado demuestra que solo es esencial que d de los colores contengan al origen [2].  Entonces, para cada vértice de la configuración de puntos, hay un simplejo heterocromático que usa ese vértice y contiene a y.  Esto demuestra automáticamente que \mu (d) \ge d+1, pero queremos más.
  • Si consideramos 2 puntos de cada color, podemos representarlos como los vértices de un octaedro en \mathbb{R}^{d+1}.  Como los simplejos heterocromáticos representan la imagen de las caras de dicho octaedro (el cual es isomorfo a una esfera), cada punto en \mathbb{R}^d está cubierto una cantidad par de veces por dichos simplejos.
Podemos ver a cada simplejo heterocromático como la imagen de alguna cara de un octaedro.

Podemos ver a cada simplejo heterocromático como la imagen de alguna cara de un octaedro.

Entonces uno puede definir una hipergráfica a partir del problema con un vértices por cada punto considerado en \mathbb{R}^d y una hiperarista (de tamaño d+1) por cada simplejo heterocromático que atrapa al punto que queremos.  Entonces, tenemos una hipergráfica con d+1 clases de vértices de tamaño al menos d+1 cada uno de tal forma que

  • Cada vértice está en al menos una arista
  • Si consideramos dos vértices de cada clase, la hipergráfica inducida por ellos tiene una cantidad par de vértices.

La idea es probar que cada hipergráfica de este tipo tiene al menos d^2+1 aristas.  Esto es lo que demuestra Sararabezolles, olvidándose de la primer condición y usando inducción sobre el mínimo número de aristas garantizadas si dicha condición sucede sólo para los vértices de k de las clases.

Les dejo el enlace al artículo de Sarrabezolles.

[1] Deza A., Huang S., Stephen T., and Terlaky T. (2006) Colourful simplicial depth. Discrete and Computational Geometry, 35, pp.597–604.

[2] Arocha, J. L., Bárány, I., Bracho, J., Fabila, R., & Montejano, L. (2009). Very colorful theorems. Discrete & Computational Geometry, 42(2), pp.142-154.

septiembre 25, 2012  

El teorema de Erdös-Ko-Rado


Si n=8, k=4, cualquier familia \mathcal{F} de 35 conjuntos que no contenga dos complementarios funciona (en la figura no hay 35).

Hace poco estuve escribiendo sobre problemas donde la estructura local de intersección de familias de conjuntos tienen consecuencias globales en la familia en sí.  Otro ejemplo muy bueno de esto es el teorema de Erdös-Ko-Rado, que habla de familias de conjuntos de tamaño fijo donde cada par de ellos se intersectan.

Lo sorprendente de este teorema es que hay una solución por Katona [1] basada en un conteo doble muy elegante, de tal manera que hace que el teorema parezca problema de olimpiada.  Lo que dice el teorema es el siguiente

Teorema (Erdös, Ko, Rado 1961) – Sean X un conjunto con n elementos y \mathcal{F} una familia de subconjuntos de X de tamaño k.  Si cada par de conjuntos en \mathcal{F} se intersectan y k \le \lfloor \frac{n}{2} \rfloor, entonces

|\mathcal{F}| \le {{n-1}\choose{k-1}}.

Ver que hay familias con {{n-1}\choose{k-1}} conjuntos es muy fácil.  Basta considerar todos los conjuntos de k elementos que tengan a cierto elemento x_0 fijo.

La idea de Katona consiste en ordenar los elementos de X en un círculo y usar el siguiente lema.

Lema – Sea X un conjunto de n elementos en un círculo.  Si \mathcal{F} es una familia de intervalos de k elementos seguidos, cada dos de ellos se intersectan y k \le \lfloor \frac{n}{2}\rfloor entonces

|\mathcal{F}| \le k.

Probar el lema no es difícil.  Una manera de hacerlo es considerar un intervalo I_0 y dividir \mathcal{F} en los intervalos que contienen al último elemento de I_0 y los que no.  Esto se puede usar para obtener la cota superior del número de intervalos.  Otra manera de hacerlo (y más referencias) se pueden encontrar en [2].

Ya con esto, probar el teorema es bastante sencillo.  Por cada manera de ordenar los conjuntos en un círculo, podemos contar cuántos conjuntos de \mathcal{F} quedan como elementos consecutivos.  Por el lema sabemos que hay a lo más k.  En el círculo hay n intervalos de k elementos consecutivos.  Entonces, si por cada manera de ordenar X en un círculo nos fijamos en los conjuntos de k elementos que están como intervalos de k elementos consecutivos, cada conjunto de k elementos está siendo contado la misma cantidad de veces.  Esto quiere decir que a lo más una proporción \frac{k}{n} de todos esos conjuntos están en \mathcal{F}.  Es decir,

|\mathcal{F}| \le \frac{k}{n}{{n}\choose{k}} = {{n-1}\choose{k-1}}.

Cabe destacar que si le imponemos más condiciones al tipo de intersecciones de los conjuntos, obtenemos condiciones mucho más fuertes sobre el tamaño de la familia.  Por ejemplo, si hay un m tal que cualesquiera dos conjuntos una familia \mathcal{F} de subconjuntos (¡de cualquier tamaño!) de X tienen exactamente m elmentos en común, entonces |\mathcal{F}| \le n.

Lo bonito de estos teoremas es que, en general, las ideas con las que se resuelven son muy elegantes.  La mejor exposición que he visto hasta ahora al respecto es por Frankl y Babai en un libro que (todavía) no sale publicado sobre métodos de álgebra lineal en problemas de combinatoria.  Conseguirlo es una lata, pero es una joya que verdaderamente la pena.

[1] – Katona, G. O. H. (1972). A simple proof of the Erdös-Chao Ko-Rado theorem. Journal of Combinatorial Theory, Series B, 13(2), 183–184.

[2] – Brouwer, A. E., & Schrijver, A. (1979). Uniform hypergraphs. Packing and Covering in Combinatorics, Mathematical Centre Tracts, 106, 39–73.

septiembre 13, 2012  

Una demostración del teorema de Tverberg


Caso k=3, d=2, 7 puntos.

El teorema de Tverberg es uno de mis teoremas favoritos en geometría combinatoria.  La idea detrás del teorema es que si uno tiene muchos puntos en \mathbb{R}^d, deberíamos poder partirlos en varios pedazos de tal forma que las envolventes convexas de cada uno tengan un punto en común.  Este teorema dice exactamente qué tantos puntos son necesarios para esto.

Desde que Tverberg dio la primer demostración de este hecho en 1966, han aparecido otras más cortas y más elegantes a lo largo de los años, con una demostración espectacular por Sarkaria en 1992.  La demostración de Sarkaria se ha difundido mucho, y encontrar textos o blogs muy buenos que la expliquen no es muy complicado (un buen ejemplo sería el blog de Gil Kalai).  Sin embargo, como no he visto ninguna versión de esto en español, y últimamente he trabajado con problemas «tipo Tverberg», creo que vale la pena dedicarle una entrada.  Lo que dice el teorema es lo siguiente:

Teorema (Tverberg 1966) – Dado un conjunto S de (k-1)(d+1)+1 puntos en \mathbb{R}^d, es posible encontrar una partición A_1, A_2, \ldots, A_k de S en k pedazos de tal forma que

\displaystyle \bigcap_{i=1}^k \langle A_i \rangle \neq \emptyset

Donde \langle X \rangle significa la envolvente convexa de X.

El caso k=2 se conoce como el lema de Radon o el Teorema de Radon, y fue demostrado en 1921.  Para este nada más se necesita álgebra lineal básica.  Curiosamente lo que hace el argumento de Sarkaria es reducir la parte combinatoria del teorema a un problema métrico.  Lo que se necesita para esto son dos ingredientes.  El primero es el teorema de Carathéodory coloreado.

Teorema (Carathéodory coloreado) – Dadas d+1 familias de puntos \mathcal{F}_1, \mathcal{F}_2, \ldots, \mathcal{F}_{d+1} en \mathbb{R}^d tales que cada una de ellas atrapa al origen, podemos encontrar puntos x_1 \in \mathcal{F}_1, x_2 \in \mathcal{F}_2, \ldots, x_{d+1} \in \mathcal{F}_{d+1} de tal forma que el conjunto \{ x_1, x_2, \ldots, x_{d+1} \} también atrapa al origen.

Con decir que un conjunto X atrapa al origen nos referimos a que 0 \in \langle X \rangle.

Este teorema es realmente métrico.  Se le llama «coloreado» porque podemos pensar que cada familia \mathcal{F}_i está pintada de algún color, y lo que queremos es un simplejo heterocromático que atrapa al origen.  Si esto no sucede, podemos considerar el simplejo heterocromático más cercano al origen y ver qué color le falta a su cara más cercana al 0.  Si todo funciona bien, demostrar que los puntos de ese color no atrapan al origen debería ser fácil.

El segundo ingrediente es el producto tensorial.  Dados dos vectores x = (x_1, x_2, \ldots, x_m) \in \mathbb{R}^m, y = (y_1, y_2, \ldots, y_n)\in \mathbb{R}^n, el producto tensorial x \otimes y es un vector en \mathbb{R}^{m \times n} tal que la entrada (i,j)-ésima es x_i y_j.  Lo único que nos interesa de este producto por el momento es que es una función bilineal de \mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R} ^{m \times n}.

Ahora sí, la idea brillante.  La idea brillante es considerar k vectores u_1, u_2, \ldots, u_k en \mathbb{R}^{k-1} que sean los vértices de un simplejo regular que atrapa al origen.  Que sea regular realmente no es tan importante, pero facilita muchísimo las cuentas.  Lo importante de estos vectores es que una combinación lineal de ellos satisface

\alpha_1 u_1 + \alpha_2 u_2 + \ldots + \alpha_k u_k = 0

si y solo si

\alpha_1 = \alpha_2 = \ldots = \alpha_k.

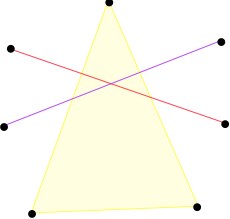
Consideremos n= (d+1)(k-1) y  a_1, a_2, \ldots, a_{n+1} nuestros puntos en \mathbb{R}^d.  Podemos agregarles a todos una entrada 1 al final.  Es decir, considerar los puntos b_i = (a_i, 1) \in \mathbb{R}^{d+1}.  Esto es un paso estándar para convertir problemas «afines» en problemas «lineales», abusando un poco del lenguaje.  Ahora consideremos los puntos b_i \otimes u_j con 1 \le i \le n+1, 1 \le j \le k.  Estos son puntos que viven en \mathbb{R}^n.  Si los acomodamos como en la figura, notemos que cada columna atrapa al origen (porque los u_i lo hacían).

Entonces, por el teorema de Carathéodory coloreado, podemos elegir un elemento de cada columna de tal forma que el conjunto que obtenemos atrapa al origen.  Es decir, para cada 1 \le i \le n+1 existe un j(i) \in \{1,2, \ldots, k\} de tal forma que el conjunto \{ b_1 \otimes u_{j(1)}, b_2 \otimes u_{j(2)}, \ldots, b_{n+1} \otimes u_{j(n+1)}\} atrapa al origen.  Los j(i) van a definir nuestra partición, por lo que conviene considerar los conjuntos I_1, I_2, \ldots, I_k tales que

I_j = \{ i \in \{ 1,2, \ldots, n+1\} : j(i) = j\}

Ahora sí, como \{ b_1 \otimes u_{j(1)}, b_2 \otimes u_{j(2)}, \ldots, b_{n+1} \otimes u_{j(n+1)}\} atrapa al origen, tenemos que hay coeficientes no negativos \beta_i que suman 1 de tal forma que

\displaystyle \sum_{i=1}^n \beta_i (b_i \otimes u_{j(i)} ) = 0

Podemos usar la linealidad del producto tensorial para factorizar los u_j, de tal forma que

\displaystyle \sum_{j=1}^k \left[ \left( \sum_{i \in I_j} \beta_i b_i \right) \otimes u_j \right] = 0

(nota: si intentan escribir la ecuación de arriba expandiendo la primer suma, el compilador de \LaTeX de wordpress se niega a hacerlo, incluso si la parten en cachos).

La magia de la demostración es que la necesidad de que los coeficientes de una combinación de los u_j que de 0 sean iguales se transfiere directamente en el producto tensorial.  Es decir,

\displaystyle \sum_{i \in I_j} \beta_i b_i

es el mismo punto para cada j.

Viendo las primeras d coordenadas, obtenemos que \displaystyle \sum_{i \in I_j} \beta_i a_i es el mismo punto para cada j.  Usando que la última coordenada es 1, obtenemos que \displaystyle \sum_{i \in I_j} \beta_i tiene el mismo valor (positivo) para cada j, por lo que podemos suponer que es 1.

Con esto obtenemos que los pedazos A_j = \{ i : i \in I_j\} forman la partición que buscabamos.

julio 22, 2012  

Helly para conjuntos finitos


Cuando empecé a escribir este blog mencioné el teorema de Helly, lo que dice es lo siguiente

Teorema 1 (Helly 1924): Sea \mathcal{F} una familia finita de conjuntos convexos en \mathbb{R}^d.  Si cada d+1 de ellos tienen un punto en común, todos los conjuntos de \mathbb{F} tienen un punto en común.

Si uno quita la condición de que los conjuntos sean convexos el teorema se vuelve claramente falso.  La idea general detrás de este teorema es la siguiente.

Dada una familia \mathcal{F} de conjuntos que satisfacen cierta propiedad \phi, propiedades «locales» sobre sus intersecciones tienen consecuencias globales sobre sus intersecciones.  El teorema de Helly es el ejemplo clásico, dónde \phi es «ser conjuntos convexos».  Los teoremas de intersecciones de convexos no son el único lugar donde este tipo de teoremas aparece.  Por ejemplo, si en vez de convexidad le pedimos a los conjuntos que ciertos grupos de homología sean triviales, el teorem se mantiene [1].  Si queremos relajar un poco la condición del teorema, ya no obtenemos una intersección de todos los conjuntos.   Sin embargo, sigue siendo interesante (y usualmente muy difícil) poder demostrar que con pocos puntos podemos interesectar a toda la familia \mathcal{F}.

Lo que quería presentar en esta entrada es una versión de este teorema pero fuera de un sentido geométrico.  Así como en \mathbb{R}^d la condición que funciona para conjuntos finitos es que todos tengan la misma cantidad de elementos.  El teorema es el siguiente:

Teorema 2 (Bollobás 1965):  Sea \mathcal{F} una familia finita de conjuntos de tamaño r.  Si para cada {{r+s}\choose{s}} de ellos existe un conjunto S' de tamaño s que los intersecta a todos, entonces existe un conjunto de S de tamaño s que intersecta a todo \mathcal{F}.

Para ver que el número {{r+s}\choose{s}} es óptimo, basta considerar \mathcal{F} como todos los subconjuntos de tamaño r de un conjunto de r+s elementos.  No es posible intersectar todos con un conjunto de tamaño s, pero sí es posible hacerlo para cualesquiera {{r+s}\choose{s}}-1.

Si el teorema no fuera cierto, podemos ir quitando conjuntos de \mathcal{F} hasta que sin importar cuál conjunto quitemos, podamos encontrar dicho conjunto S.  Supongamos que en este momento los elementos de \mathcal{F} que quedan son A_1, A_2, \ldots, A_m.  Sabemos que al quitar cualquier A_i podermos encontrar un conjunto B_i de tamaño s que intersecta a todos los otros A_j.  Como todo \mathcal{F} no podía ser intersectada con un conjunto de tamaño s, tenemos que A_i y B_i son disjuntos.  Además, sabemos que m > {{r+s}\choose{s}}.  Con esto, basta demostrar lo siguiente:

Teorema 3 (Bollobás 1965).  Sean A_1, A_2, \ldots, A_m conjuntos de tamaño r y B_1, B_2, \ldots, B_m conjuntos de tamaño s tales que A_i \cap B_j \neq \emptyset si y solo si i \neq j.  Entonces m \le {{r+s}\choose{s}}.

La siguiente demostración es de Lovász y hace uso del álgebra exterior (cosa que es sorprendente si consideramos que el problema es completamente combinatorio).

Demostración: Sea X la unión de todos los A_i y B_i.  Sin pérdida de generalidad podemos considerar que X es un subconjunto de \mathbb{R}^{r+s} de tal forma que cualesquiera r+s puntos de X son linealmente independientes.  Dado U = \{u_1, u_2, \ldots, u_k\} definimos \wedge_U = u_1 \wedge u_2 \wedge \cdots \wedge u_k el producto exterior de sus elementos.  Vamos a demostrar que \wedge_{A_1}, \wedge_{A_2}, \ldots, \wedge_{A_m} son linealmente independientes.  Para eso consideremos una combinación lineal de ellos que dé 0, es decir

( \lambda_1 \wedge_{A_1}) + \lambda_2 (\wedge_{A_2}) + \ldots + \lambda_m (\wedge_{A_m}) = 0

Si consideramos el producto exterior con \wedge _{B_i} tenemos que (\wedge_{A_j})\wedge (\wedge_{B_i}) es el producto exterior de todos los elementos de A_j y B_i.  Si i \neq j, hay al menos un elemento repetido en este producto exterior, por lo que da 0.  Esto implica que

\lambda_i [(\wedge_{A_i})\wedge(\wedge_{B_i})] = 0.  Como A_i \cup B_i es un conjunto linealmente independiente, el producto exterior de sus elementos no es 0, por lo que \lambda_i = 0.  Con esto tenemos que todos los coeficientes son 0, por lo que los \wedge_{A_i} son linealmente independientes.

Sin embargo, cada uno de ellos es el producto exterior de r elementos de W, por lo que están en un espacio vectorial de dimensión {{\mbox{dim }W}\choose{r}} = {{r+s}\choose{s}}.  Con esto, no puede haber más de  $latex {{r+s}\choose{s}}$ de ellos, como se quería probar.

[1] Debrunner, H. (1970). Helly type theorems derived from basic singular homology. The American Mathematical Monthly, 77(4), 375–380.

abril 12, 2012  

Una demostración sencilla del teorema de Borsuk-Ulam


El teorema de Borsuk-Ulam es una herramienta topológica realmente padre por varias razones

  1. Es fácil de describir
  2. Tiene muchas equivalencias
  3. Tiene muchas demostraciones
  4. Tiene muchas aplicaciones dentro de otras áreas (como geometría discreta)
De hecho, cada vez que se logra usar este teorema suele dar lugar a demostraciones muy bonitas, a tal grado que hay libros increíbles como [1] dedicados a esto.  Lo que dice es lo siguiente:
febrero 11, 2012  

Conteos dobles y álgebra lineal.


familias de subconjuntos

Hace poco me encontré con un par de problemas que a primera vista parecen problemas de conteo doble, tipo olimpiada, pero resulta que salen con álgebra lineal.  Me refiero a que parece tipo olimpiada porque hay problemas semejantes que han aparecido en estos concursos.  Por ejemplo

Lista corta para la IMO 2004 C1:  Hay 10001 estudiantes en una universidad.  Los estudiantes se juntan en pandillas (un estudiante puede estar en varias pandillas) y las pandillas se juntan en sociedades (una pandilla puede estar en varias sociedades).  Supón que hay k sociedades y que se cumple lo siguiente:

  • Cada pareja de estudiantes está en exactamente una pandilla.
  • Por cada estudiante y cada sociedad, el estudiante pertenece a exactamente una pandilla de la sociedad
  • Cada pandilla tiene una cantidad impar de estudiantes.  Además, si una pandilla tiene 2m+1 estudiantes (con m un entero no negativo), entonces está en exactamente m sociedades.

Encuentra todos los valores posibles de k.

Solución.

Sea a un estudiante fijo.  Vamos a contar el número de parejas (P,S) tales que S es una sociedad y P es una pandilla tales que a pertenece a P y P pertenece a S.  Por la segunda condición, por cada sociedad hay exactamente una de estas parejas, por lo que hay k parejas.  Ahora vamos a contar por pandillas.  Si en una pandilla P_0 está a, debe haber otras 2m personas para alguna m entera no negativa.  Entonces hay m parejas de la forma (P_0,S).   Como a estás en exactamente una pandilla con cada uno de los otros 10000 estudiantes, al variar P_0 obtendremos exactamente 5000 de estas parejas.  Entonces el único valor posible de k es 5000.  Además, si sólo hay una pandilla con los 10001 estudiantes y 5000 sociedades iguales (todas formadas por la única pandilla) es claro que todas las condiciones del problema se cumple.  Entonces k=5000 funciona.

La idea en general es sencilla.  Se nos da información sobre dos o tres conjuntos finitos donde uno representa subconjuntos de otro, y se nos dan algunas propiedades sobre la estructura de estos.  Un conteo doble que logra usar de manera separada las propiedades nos da mucha información sobre el conjunto.  Viendo este tipo de problemas, es natural intentar usar este tipo de herramientas en el siguiente problema.

Problema.  En una ciudad con n personas, la gente forma sociedades.  Se sabe que cada sociedad tiene una cantidad impar de personas y cada par de sociedades tienen una cantidad par (posiblemente 0) de personas en común.  Demuestra que hay a lo más n sociedades.

La idea para resolver este problema (con la solución que conozco) sigue siendo un conteo doble, pero bastante más escondido.

Solución.  Supongamos que hay m sociedades.  Consideremos una matriz A de m \times n con entradas 0 ó 1.  la entrada a_{i,j} va a ser 1 ó 0 dependiendo si la persona j está o no (respectivamente) en la sociedad i.  Podemos considerar la matriz como una cuyos elementos están en el campo \mathbb{Z}_2 (para simplificar los argumentos a la hora de multiplicar.  Ahora consideremos la matriz B=AA^{\perp}.  Es una matriz de m \times m cuya entrada  b_{i,j} \in \{0,1\} nos dice la paridad de personas que están tanto en la sociedad i como en la sociedad j.  Por lo tanto (dadas las condiciones del problema), es la matriz identidad.  Con esto tenemos que su rango es m.  Por otro lado, como es el producto de dos matrices de rango a lo más n (porque A es de n \times n), su rango es a lo más n.  Por lo tanto m \le n, como queríamos.

Al final de cuentas esta solución sigue siendo un conteo doble, contando de dos maneras el rango de B.  Sin embargo, me parece que (a pesar de que la solución es muy elegante y corta) debería poder resolverse usando pura combinatoria básica.  Realmente lo único que falta es una descripción combinatoria de qué significa realmente el rango de A, pero tampoco quiero una solución que parezca una traducción forzada.  A veces en problemas de combinatoria las soluciones más elegantes son usando resultados de otras áreas, como la solución de Lovász de la conjetura de Kneser.  Este es un resultado importante de combinatoria que se resuelve de manera muy impresionante con topología algebraica.  Sin embargo, en este ejemplo no creo que tener que recurrir al álgebra lineal sea necesario.

El problema y la solución los conseguí del libro «thirty-three miniatures» de Jiří Matoušek.  Ahí vienen muchas más aplicaciones bonitas (32 otras, como es de esperarse del título) de este tipo de herramientas a problemas en combinatoria.

abril 4, 2010  

Teoría de números y geometría


Cuando uno logra hacer una prueba interdisciplinaria en matemáticas suele tener un grado de elegancia bastante particular.  Como hace rato que no hago una entrada voy a presentar una de mis pruebas favoritas.

Hoy quería presentar cómo se puede ver de manera exclusivamente geométrica que todo primo p se puede escribir de a lo más una manera como suma de dos cuadrados.

Para probar esto, supongamos lo contrario.  Es decir, tenemos un primo p = a^2 + b^2 = c^2 + d^2 y vamos a probar que \{ a, b\} y \{c,d\} son la misma pareja.

Entonces podemos trazar un cuadrilátero A, B, C, D de tal manera que

AB = a, BC= b, CD=c, DA= d, AC= \sqrt{p}

Entonces por Pitágoras tenemos que \triangle ABC, \triangle ADC son rectángulos.  Con esto el cuadrilátero ABCD es cíclico y está inscrito en un círculo con diámetro \sqrt{p}.

Si le llamamos r a la longitud del segmento BD por Ptolomeo tenemos lo siguiente:

r\sqrt{p} = ac + bd

A partir de aquí hay dos maneras de proseguir, la más sencilla es usando una ley de cosenos en el triángulo \triangle ABD, pero para uno de los pasos se necesita un manejo (mínimo) de congruencias, por lo que voy a seguir por el lado geométrico.  En este caso también vamos a tratar de calcular r.

Primero denotemos \angle BAC = \theta_1, \angle CAD = \theta_2, \angle ABD = \angle ACD = \gamma_2, \angle ADB = \angle ACB = \gamma_1.  Por los triángulos rectángulos conocemos todos los senos y cosenos de estos ángulos.  Llamémosle X a la intersección de AC, BD y sean u = BX, v = XD, t = AX.

Ahora sí, si aplicamos ley de senos a \triangle ABX obtenemos que

\frac{u}{t} = \frac{\sin{\theta_1}}{\sin{\gamma_2}}=\frac{b}{d}

De la misma manera obtenemos que v= \frac{tc}{a}.  Con lo que tenemos

r = u+v = t\left( \frac{ab+cd}{ad} \right)

Además, por potencia desde X tenemos que t (\sqrt{p} - t) = uv = t^2 \left( \frac{bc}{ad} \right).  De aquí podemos se cancela una t y al despejar esta variable obtenemos que t = \frac{ad}{bc+ad}\sqrt{p}

Juntando esto y la ecuación anterior obtenemos que

r = \sqrt{p} \left (\frac{ab+cd}{bc+ad} \right)

Al juntarlo con la fórmula de ptolomeo y despejar p nos queda

p = \frac{(ac+bd)(ad+bc)}{ab+cd}

Con esto tenemos que alguno de ac+bd y ad+bc es múltiplo de p (¡Ésto el lo único que vamos a usar de teoría de números!).  Como podemos intercambiar en nuestro cuadrilátero original donde van c y d podemos suponer que el múltiplo es ac + bd y quedarnos con la construcción original.  Entonces p \le ac + bd = r \sqrt{p}.  Pero como AC era diámetro de nuestro círculo circunscrito obtenemos que r = \sqrt{p}.

De aquí nuestro cuadrilátero es un rectángulo, por lo que a=c y b=d, que es lo que queríamos.

marzo 26, 2010  

Un problema de isometrías


Ahora quería presentar un problema bastante bonito, que habla sobre isometrías sin puntos fijos.  Una isometría es una función que preserva distancia.

Problema: Dada isometría f: \mathbb{R}^d \longrightarrow \mathbb{R}^d tal que para todo x \in \mathbb{R}^d se cumple que f(x) \neq x entonces podemos encontrar una recta l tal que f[l] = l.

Aquí estamos tomando a \mathbb{R}^d con su métrica usual.  Un ejemplo clásico de isometría sin puntos fijos es una transalción.  En este caso queda claro que cualquier recta con la misma dirección que la traslación queda fija.

Para probar este problema, primero vamos a ver qué pasa si encontramos un punto x tal que a=|| f(x) - x || es mínimo.

Notemos que si x, f(x), f(f(x)) son colineales, ya acabamos, porque mandaríamos la recta que pasa por x, f(x) a la recta que pasa por f(x), f(f(x)), que es la misma.  Si no es la misma entonces consideremos t el punto medio de x, f(x).  Este punto debe ir al punto medio de f(x), f(f(x)).

Con esto, si le aplicamos la desigualdad del triángulo al que tiene vértices t, f(x), f(t), como es un triángulo no degenerado obtenemos que

a = \frac{a}{2} + \frac{a}{2} = ||t-f(x)|| + ||f(x) - f(t)|| > ||t - f(t) ||

Esto contradice la minimalidad de a por lo que hemos acabado.

Ver que el mínimo a realmente existe es un poco técnico por lo que lo dejé al final.  Resulta que toda isometría en \mathbb{R}^d se puede ver de la forma f(x) = Mx + b.  Donde M es una matriz con ciertas propiedades y b es un vector.  Con esto f(x) - x = (M-I) x + b.  Usando esto se puede reducir el problema de encontrar un mínimo a encontrarlo en cierta esfera centrada en el origen, por lo que como estamos en un compacto eso existe.

marzo 16, 2010  

El problema 5 de la IMO 2006


Hoy quería ver una solución a un problema de polinomios que apareció en una imo reciente, lo que dice es lo siguiente:

Problema: Sea P(x) un polinomio con coeficientes enteros y grado n \ge 2.  Sea k un entero positivo.  Demuestra que hay a lo más n enteros a tales que P^k (a) = a.

Nota: P^k (a) se refiere a P(P(P(\ldots P(a))\ldots) donde la P se aplicó k veces.

Cuando k=1 el problema es trivial, ya que los números que cumplen serían raíces del polinomio P(x) - x, el cuál tiene grado n.  Sin embargo, para k más grande hay que usar las condiciones extras, en este caso sólo tenemos lo de coeficientes enteros y que los números que buscamos son a su vez enteros.

La base para resolver este problema es la siguiente:

Sabemos que a-b | a^r - b^r para todo r entero positivo.   Con esto a-b | P(a)-P(b).  Con esto si a y b son enteros que cumplen la condición tenemos que (abusando un poco de la notación)

a - b | P(a)-P(b) | P^2(a)-P^2(b) | \cdots | P^k (a)-P^k(b) = a-b

Con esto tenemos que todos los números en la lista tienen el mismo valor absoluto, en particular

|a-b| = |P(a)-P(b)|

Entonces P(a) y P(b) están a la misma distancia, y lo único que puede cambiar es si están en el mismo orden o no.  Es claro que si tenemos al menos 3 de estos números, los tres deben preservar su orden o los 3 se deben voltear (para preservar todas las distancias), por lo que usando un argumento inductivo, todos los números que cumplen esto preservan su orden o lo voltean.

Entonces hay un real r tal que P(x) = x + r o P(x) = -x + r para todo x entre los números que cumplen la condición.

Entonces todos los números que cumplen la condición son raíces de un polinomio de la forma P(x) - x -r o P(x) +x -r.  Como P(x) tiene grado n \ge 2 ese polinomio también, por lo que hay a lo más n números que cumplan la condición, por lo que hemos acabado.

Para ver que la condición n \ge 2 es necesaria$, si consideramos el polinomio P(x) = x y cualquier k o $P(x) = -x + t$ (con cualquier t) y cualquier k par, todos los enteros cumplen lo que buscabamos.

febrero 18, 2010  

Producto cruz y geometría euclidiana


El producto cruz es una función \times : \mathbb{R}^3 \times \mathbb{R}^3 \longrightarrow \mathbb{R}^3 tal que produce un vector ortogonal a dos vectores dados, cuya norma es igual al doble del área del triángulo que forman esos dos vectores con el origen.

Es raro ver una aplicación de este tipo de herramientas en problemas de geometría moderna, sobre todo cuando tratan problemas en el plano, pero aquí va un ejemplo.

Problema : Sea \triangle ABC un triángulo en el plano con ortocentro H y circuncentro O.  Demuestra que hay dos de los triángulos \triangle AOH, \triangle BOH, \triangle COH cuyas áreas suman la del tercero.

Solución con geometría moderna:

Como todos los triángulos tienen la misma base OH, sólo hay que demostrar que las longitudes de las alturas correspondientes cumplen lo que queremos.  Sabemos que el segmento OH pasa por el gravicentro G.  Digamos que esta recta deja al vértice A de un lado y a B, C del otro.  Si consideramos M el punto medio de BC, entonces el segmento AM intersecta a OH en G.  Eso quiere decir que la altura desde A es el doble que la de desde M, la cual es el promedio de las alturas desde B, C.  Con esto hemos terminado.

Solución usando el producto cruz.

Si consideramos el origen en O, tenemos que H = A + B + C.  Imaginemos que el plano está encajado en \mathbb{R}^3, por lo que ahora tiene sentido el producto cruz.  Notemos que las áreas de los triángulos que queremos son la mitad de las normas de A \times H, B \times H, C \times H y que estos últimos vectores son paralelos (por ser ortogonales al plano de A, B, C).  Además como

A \times H + B \times H + C \times H = (A+B+C) \times H = (A + B + C) \times (A + B + C) = 0

obtenemos lo que queríamos.

« Older Posts